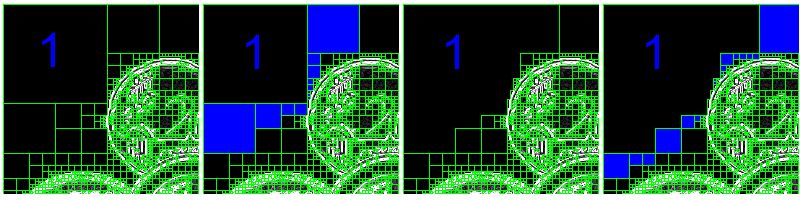
III. Décomposition/Fusion (Split/Merge)▲
Cette technique enchaîne les 2 phases suivantes :
1. Découper itérativement l'image jusqu'à avoir des blocs contenant exclusivement des pixels similaires.
2. Regrouper les blocs voisins s'ils sont similaires
Les deux phases sont nécessaires afin de garantir que les régions obtenues sont à la fois homogènes et également les plus grandes possibles. Chaque phase étant indépendante, on peut les étudier séparément.
La décomposition (split)
La méthode couramment utilisée consiste à faire une dichotomie par blocs de l'image. Pour cela, on commence par définir un bloc de la taille de l'image, puis on examine le contenu de ce bloc. Si le bloc est homogène (= contient exclusivement des pixels similaires) alors on arrête la décomposition. Sinon, on découpe le bloc en 4 sous-blocs et on examine le contenu de chaque sous-blocs.
Et ainsi de suite jusqu'à ce qu'il n'y ait plus besoin de décomposer les blocs. Le résultat obtenu est donc un ensemble jointif de blocs de différentes tailles qui recouvre entièrement l'image.
L'implémentation la plus simple pour cette méthode consiste à définir une structure d'arbre appelée QuadTree. C'est un arbre dans lequel chaque nœud représente un bloc. Chaque nœud possède donc 0 sous-nœud (bloc homogène) ou 4 sous-nœuds (bloc non-homogène).
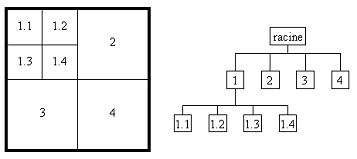
La décomposition finale est définie par les blocs associés aux feuilles de l'arbre. On obtient ainsi une liste de blocs de différentes tailles et positions. Si la structure du QuadTree permet une navigation aisée entre bloc conteneur (parent) et sous-blocs (enfants), elle ne permet pas de naviguer facilement entre des blocs voisins.
Pour cela, il est préférable de construire et d'utiliser le graphe d'adjacence.
La sur-segmentation (over segmentation)
La méthode de décomposition décrite ci-dessus entraîne la création systématique de 4 sous-blocs en cas de non-homogénéité. Cependant, dans les dernières itérations, la décomposition en 4 sous-blocs n'est normalement pas nécessaire. En effet, parmi les 4 sous-blocs créés, plusieurs sont similaires.
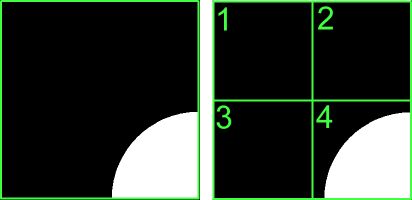
De plus, chaque bloc étant traité isolément de ses voisins, certains sous-blocs, parfois de tailles différentes, seront à la fois similaires et jointifs.
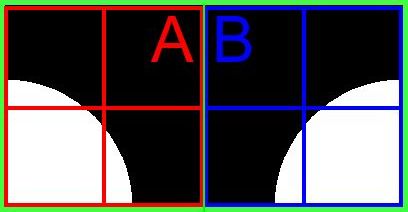
Au final, l'image va contenir de nombreux petits blocs jointifs et similaires. Ce phénomène, inhérent à la méthode de décomposition, s'appelle la sur-segmentation. La prochaine étape de l'algorithme va donc être de regrouper les blocs jointifs et similaires en une seule région.
La fusion (merge)
Cette étape à pour objectif d'identifier les régions qui composent l'image en regroupant les blocs jointifs et similaires.
Il faut tout d'abord définir le critère de similarité entre blocs. Le plus simple est d'étendre la définition de similarité entre pixels définie lors de l'étape de décomposition. Ainsi, on peut assimiler un bloc à un " gros " pixel en calculant sa valeur/couleur moyenne, et en utilisant le graphe d'adjacence pour naviguer vers les blocs voisins.
L'algorithme de la fusion est un procédé itératif:
Créer la liste « [K] » des blocs associés aux feuilles du QuadTree
Pour chaque bloc « B » dans la liste « [K] »
Créer une nouvelle région « [R] »
Retirer « B » de « [K] » et l'ajouter dans « [R] »
Calculer la valeur/couleur moyenne de « [R] »
Créer la liste « [N] » des blocs voisins du bloc « B »
Pour chaque bloc « Bn » dans la liste « [N] »
Si (« Bn » est dans « [K] ») ET (« Bn » et « [R] » sont similaires) Alors
Retirer « Bn » de « [K] » et l'ajouter dans « [R] »
Ajouter les blocs voisins de « Bn » dans la liste « [N] »
Recalculer la valeur/couleur moyenne de « [R] »
Fin Si
Fin Pour
Fin Pour
Cet algorithme construit les régions une par une, en regroupant progressivement les blocs jointifs autour d'un bloc de départ. L'algorithme amalgame les blocs adjacents à la région, formant ainsi une région de plus en plus grande.
Il est conseillé de trier les blocs de la liste " K " par taille décroissante. L'algorithme commence ainsi par construire les régions en commençant par les plus grands blocs, ce qui améliore la stabilité du calcul de la valeur/couleur moyenne de la région.
|
|
| Résultat intermédiaire de la fusion. On construit d'abord les grandes régions | Résultat final de la fusion (1926 régions) |